The
Days of the Week:
An Exercise In
Theory of Mind
James
Williams
Originally written in 2000 at age 12, revised multiple times
afterwards.
Throughout
history, there are people—some of whom are on the autism spectrum—that have
been called "savants."
What
is a savant? A savant is someone who is very skilled
at an area that is believed to be useless for any practical purposes. Those
areas are called “splinter skills,” and savants are often punished for boring
people about the thing that they obsess in.
Ironically,
most people know very little as to how a savant is able to
do what he or she can do, yet many people make fun of them for their abilities.
This is yet another example of when a normal person lacks a theory of mind
toward an autistic person, not the other way around.
One
well-known savant skill is the ability to tell you what the day of the week any
calendar date is on if you ask them (in a matter of seconds). For example, if
you tell them you were born on August 1, 1989, they could tell you that it was
a Tuesday. But if you ask them how they did it, very few savants could explain
to you how—just as you might have a hard time explaining why you know social
skills from your heart and an autistic person has a hard time learning.
I’m
not a savant, and I couldn’t do that in a matter of seconds. But I sat down one
day, in the summer of 2000, and analyzed the weekdays in calendar dates and
found that they followed specific patterns. I realized that there is a method
that can explain how this is done. It requires memorizing a system of patterns
and mathematical algorithms.
Since
2000, when I originally wrote my ideas, they have changed as I have learned
more about our calendar. I learned that the calendar used in the United States
and many other countries is technically called the Gregorian calendar,
and have periodically edited the algorithms after being notified of inaccuracies
by other autistic people or noticing them myself.
There
are likely a lot more ways to solve this problem, and numerous variations on
each way. However, to most people, how to find out what day of the week a
calendar date fell on is a mystery. Here I will show you one way to solve this
problem, with a combination of patterns and mathematics.
So,
without further ado, in an exercise regarding theory of mind, you are about to
see a mathematical explanation to the art of finding weekdays on dates in the Gregorian
calendar.
Introduction
So,
how do you find out what day of the week a specific date was on?
Dates
are split up into three parts—-months, days, and years. For example:
In
this date, December is the month, 12 is the day, and 1965 is the year. Now, we
need to find another calendar date where we have memorized what weekday it was
on. From there we can find out what weekday 12/12/1965 fell on.
The
simplest way to do that is if we know what weekday December 12th
fell on in another year. Then we can simply count down from that year to 1965.
But since that is not always an option, let’s pick a random date:
Although
every day of the week is given at least one opportunity to be the 1st
of a specific month within each calendar year, there are months within each
year that share days of the week. Because of this, we do not have to count each
month from January to December.
However,
those months differ depending on whether or not the
year is a leap year or not. The following are the rules regarding which months
share days of the week throughout the year—whether or not
it is a leap year or a common year:
IN
LEAP YEARS:
January,
April, and July share the same weekdays.
March
and November share the same weekdays.
February
and August share the same weekdays.
October
does not share a weekday with any other month.
IN
COMMON YEARS:
January
and October share the same weekdays.
April
and July share the same weekdays.
February,
March, and November share the same weekdays.
August
does not share a weekday with any other month.
IN
ALL YEARS:
September
and December share the same weekdays.
May
and June do not share a weekday with any other month.
So the first question is—is 2003 a leap
year?
Leap
years must follow two criteria. They must be divisible by 4, but they cannot
be divisible by 100 unless they are also divisible by 400.
For
example, even though 1700, 1800, and 1900 are divisible by 4, they are not leap
years because they are also divisible by 100. But 1600 and 2000 are leap years
since they are not only divisible by 4 and 100, they are also divisible by 400.
However, all years that are divisible by 4 that are not divisible by 100 or 400
are leap years. Thus, 1936 is a leap year.
So,
is 2003 a leap year? Let’s divide 2003 by 4.
2003 / 4 = 500.75
2003
is not divisible by 4. It is also not divisible by 100 or 400 since all numbers
divisible by 100 or 400 must end in 0, and 2003 ends in 3.
Thus,
it is a common year. With this information we can conclude:
January
2003 and October 2003 share the same weekdays.
Thus,
October 23, 2003 starts on a Thursday.
We
can use this information to find out when December 23, 2003 starts.
How
do we find this information? All dates on the next month of the year start on a
predictable weekday based on the weekday of the date of the current month being
analyzed and how many days are in that same month, utilizing the following formulas:
If
the current month has 31 days (January, March, May, July, August, October,
December), the next month starts three weekdays after the current month,
as follows:

If
the current month has 30 days (September, April, June, November), the next
month starts two weekdays after the current month.

If
the current month has 29 days (February on leap years), the next month starts one
weekday after the current month.

If
the current month has 28 days (February on non-leap years), the next month
starts the same weekday as the current month.
This
is because 28 days is equal to 4 full weeks, and 29, 30, and 31-month days have
extra days along with the 7-day 4 weeks.
October
is a 31-day month. Thus, November 23rd starts three weekdays after October 23rd.
10/23/2003 is on a
Thursday.
Thus, 11/23/2003
starts on a Sunday.
November
is a 30-day month. Thus, December 23rd starts two weekdays after November 23rd.
11/23/2003 is on a
Sunday.
Thus, 12/23/2003
starts on a Tuesday.
Now
we know that December 23, 2003 falls on a Tuesday. We can now use this
information to find out what day December 1, 2003 was on. Then we can find out
what December 12, 2003 started on.
A
month consists of at least four weeks. As there are seven weekdays, and thus
seven days in a week, the next day that repeats the weekday is seven days apart
from a previous day. For example, If December 23rd starts on a
Tuesday, then December 30th starts on a Tuesday.
We
can determine what day of the week December 1st started on from December 23rd
by analyzing how many weekdays we must add or subtract from the 23rd of the
month’s weekday, based on this formula:
If
the day is the 8th, 15th, 22nd, or 29th
in the month, it falls on the same weekday as the 1st of the month.
If
the day is the 2nd, 9th, 16th, 23rd,
or 30th in the month, it falls on the first weekday after the 1st
of the month’s weekday.
If
the day is the 3rd, 10th, 17th, 24th,
or 31st in the month, it falls on the second weekday after the 1st
of the month’s weekday.
If
the day is the 4th, 11th, 18th, and 25th
in the month, it falls on the third weekday after the 1st of the
month’s weekday.
If
the day is the 5th, 12th, 19th, or 26th
in the month, it falls on the third weekday before the 1st of the
month’s weekday.
If
the day is the 6th, 13th, 20th, or 27th
in the month, it falls on the second weekday before the 1st of the
month’s weekday.
If
the day is the 7th, 14th, 21st, or 28th
in the month, it falls on the weekday before the 1st of the month’s
weekday.
This
means that December 1st starts one weekday before December 23rd. Since December
23rd starts on a Tuesday:
Go back one
weekday from Tuesday = Monday
This
means December 1st, 2003 fell on a Monday. With the same formula, we can find
out what December 12th, 2003 fell on.
Looking
back, we see that December 12th falls on the third weekday before the 1st of
the month. Since December 1st starts on a Monday:
Go down three weekdays
from Monday = Sunday, Saturday, Friday
December
12, 2003, fell on a Friday. Now we can find out what day of the week December
12, 1965 fell on.
The
Year Cycles
Most
dates on the Gregorian calendar follow a distinct weekday cycle, year by year. Although
the Gregorian calendar completes its full cycles of weekdays and months every
400 years, a typical weekday cycle usually takes 28 years to complete, since there
are 7 distinct weekdays, and because leap years typically occur every 4 years
(except when, as mentioned above, the year is divisible by 4 and 100, wherein a
leap year does not occur for 8 years, such as from 1896 to 1904). As a result,
the 28 year weekday cycle happens uniformly unless it
is disrupted by the absence of a leap year, which occurs three times during the
typical 400-year cycle of the Gregorian calendar. Indeed, although February 29th
only occurs on leap years and has a different counting pattern compared other
dates on the calendar, it is still subject to the same 28
year weekday cycle and subsequent disruptions caused by the leap year
discrepancy mentioned above.
Therefore—if
you are counting forward or back the weekdays of any given date by year to
figure out a specific calendar date, and you are not going past any of the
common years that are divisible by 4 and 100, you are free to jump from the
weekday you are starting from up or down every 28 years, since it will be the
same weekday. If, however, you are going past one of those common years, you
will need to count up or down weekdays, one year by one year, until the weekday
cycle has resumed itself (which will vary, based on what year or date you are
looking for). Likewise, if the year you are counting up
or down to is less than 28 years before or after the year you are starting
form, you will also need to count up or down weekdays one year by one year as
well. For February 29th, this would mean counting
up or down each leap year, with the same rules of the weekday cycle as
mentioned above.
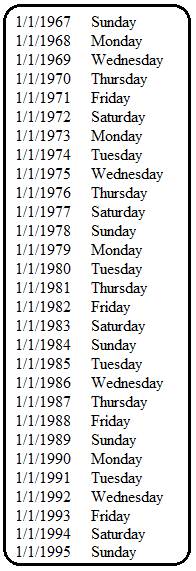
Example
1: The year 1967 started on a Sunday, which was a common year. 1995 is 28 years
after 1967. Since no common years that are divisible by 4 and 100 occur between
1967 and 1995, the year 1995 also started on a Sunday, which was also a common
year. Here is the cycle from 1967 to 1995:
Example
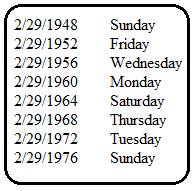
2: February 29th, 1948 occurred on a Sunday. 1976 is 28 years after
1948. Since no common years that are divisible by 4 and 100 occur between 1948
and 1976, February 29th, 1976 also occurred on a Sunday. Here is the
cycle from 1948 to 1976:
This
information can be utilized to find out what weekday a specific date falls on
in each year compared to another year and can be used to determine our target date—December
12, 1965—from December 12, 2003. As mentioned above, December 12, 2003, fell on
a Friday.
Since
no common years that are divisible by 4 and 100 occur between 2003 and 1965
(2000 was a leap year since it is divisible by 4, 100, and 400, and completed
the 400-year cycle between 1600 and 2000), the 28 year weekday cycle is not
disrupted between 2003 and 1965. Therefore, we can use this cycle to simplify
the process of counting down weekdays from 2003 to 1965. First, we must
subtract 1965 from 2003 to find out how many years ago 1965 was from 2003.
2003 – 1965 = 38
Therefore, we do not need to individually
count down all 35 years to find out what weekday 1965 started on. We can jump
28 years from 2003 and then count individual years from there.
So now we must subtract 28 from 2000 to
find out what year that is.
2003 – 28 = 1975
This
means that like in 2003, December 12, 1975 also started on a Friday, which is
also a common year.
However,
we cannot jump any further from here because 1965 is only 10 years from 1965,
and 10 is less than 28.
So we now can count down years from 1975 to
1965. But how do we do that?
To
count up or down weekdays, one by one, with a specific dates
between years, one of three counting patterns must be used, depending on the
date.
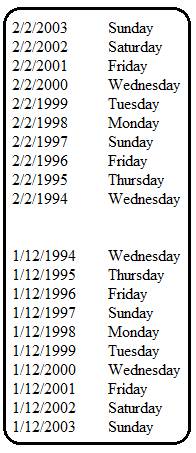
If
you are counting down or up with a date before February 29th, each date occurs
one weekday earlier (if counting down) or one weekday later (if counting up)
between common years, and between a leap year and a preceding common year (if
counting down) or between a common year and a following leap year (if counting
up). Each date occurs two weekdays earlier between a common year and the preceding
leap year (if counting down), or two weekdays later between a leap year and the
following common year (if counting up). For example:
If
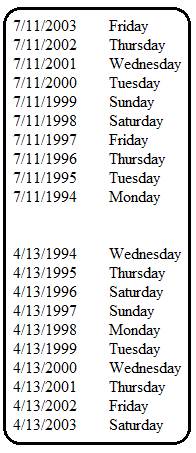
you are counting down or up with a date after February 29th, each date occurs
one one weekday earlier (if counting down) or weekday
later (if counting up) between common years, and between a common year and a
preceding leap year (if counting down) or between a leap year and a following common
year (if counting up). Each date occurs two weekdays earlier between a leap
year and the preceding common year (if counting down), or two weekdays later between
a common year and the following leap year (if counting up).
For example:
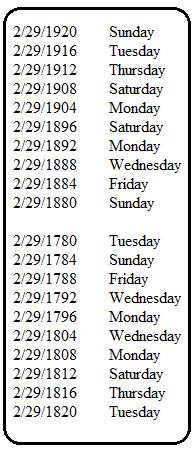
If
you are determining a weekday for February 29th (which date occurs
every leap year), the following counting patterns apply. If the leap years are
4 years apart, February 29th occurs two weekdays after each preceding
February 29th (if counting down), or two weekdays before each
following February 29th (if counting up).
If the leap years are 8 years apart (such as between 1896 and 1904), February
29th occurs two weekdays before each preceding February 29th
(if counting down), or two weekdays after each following February 29th
(if counting up). For example:
Now
we can get back to our original quest of looking for the day of the week that December
12th, 1965 occurred on. Since December 12th is after February
29th, when counting down, we follow the counting pattern of dates
after February 29th mentioned above. And we already know that December
12th, 1975 fell on the same weekday that December 12th, 2003
fell on.
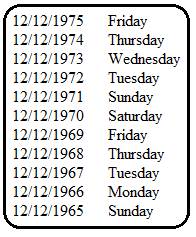
We
also know that as we count down from 1975 to 1965, we will pass two leap years:
1972 and 1968.
So,
now let’s count down:
And
this means that December 12, 1965 fell on a Sunday.
And
that’s how you find out the day of the week for a specific date. There are also
likely to be other methods that exist as well.